You are amazing, you earn a lot.

Fang Sanwen's Chat Record - Reading "You Are Amazing, You Earn a Lot" · Tang Qiao's Blog

Introduction Recently finished reading "You Are Amazing, You Earn a Lot" by Fang Sanwen, CEO of Xueqiu.

Introduction#

Recently finished reading "You Are Amazing, You Earn a Lot" by Fang Sanwen, CEO of Xueqiu. This is a rather special book, as much of its content is presented in the form of chat records on Xueqiu, which makes it feel less systematic. However, if a book can provide readers with several points of reflection and summary, it is worth the price and time.

The entire book has brought me quite a few thoughts, and here are some notes.

What is a Gambler#

The section in the book about "the stock market and gamblers" made me ponder what a true value investor is. I found that, in fact, almost all investments carry a gambling component.

We might typically think there are two ways to make money in stocks:

Make money from the market
Make money from trading partners

However, even so-called value investors buy stocks when the target stock price is reasonable or extremely low. At that point, if they indeed achieve returns that exceed the average rate of return, the premise is that they assume both they and their trading partners are fools, and indeed they are. So, they are also making money from trading partners.

At the same time, when you buy a stock, you are actually doing two things: stock selection and timing. Both of these actions have significant uncertainties:

No one can predict the future ups and downs of a stock, so your timing is a form of gambling.
No one can obtain all the information about a company; decisions are made under conditions of incomplete information. The investment decision made at this time, although referenced by a lot of information, is still a gamble due to its incompleteness.

The only possible investment that might not involve gambling is index investing, as it gives up stock selection and timing; it purely makes money from the market, while others do not.

Gambler's Ruin Problem Research Summary | YorkFish Blog

Introduction#

The following is a research summary of the "Gambler's Ruin" series of problems. Through mathematical proof, it can be seen that "nine out of ten gamblers lose" is not an empty phrase.

PS: Since Markdown does not support mathematical formulas, the proof process for the following problems is written using Daum Equation Editor and then exported as images for display.

Probability of the Banker Losing All Chips#

The banker has n chips, and each time has a probability p of winning a chip or a probability q (q=1-p) of losing a chip. The game ends when the banker loses all their money. Assuming each gambling instance is independent, find the probability that the banker loses all their chips.

The answer is as follows:

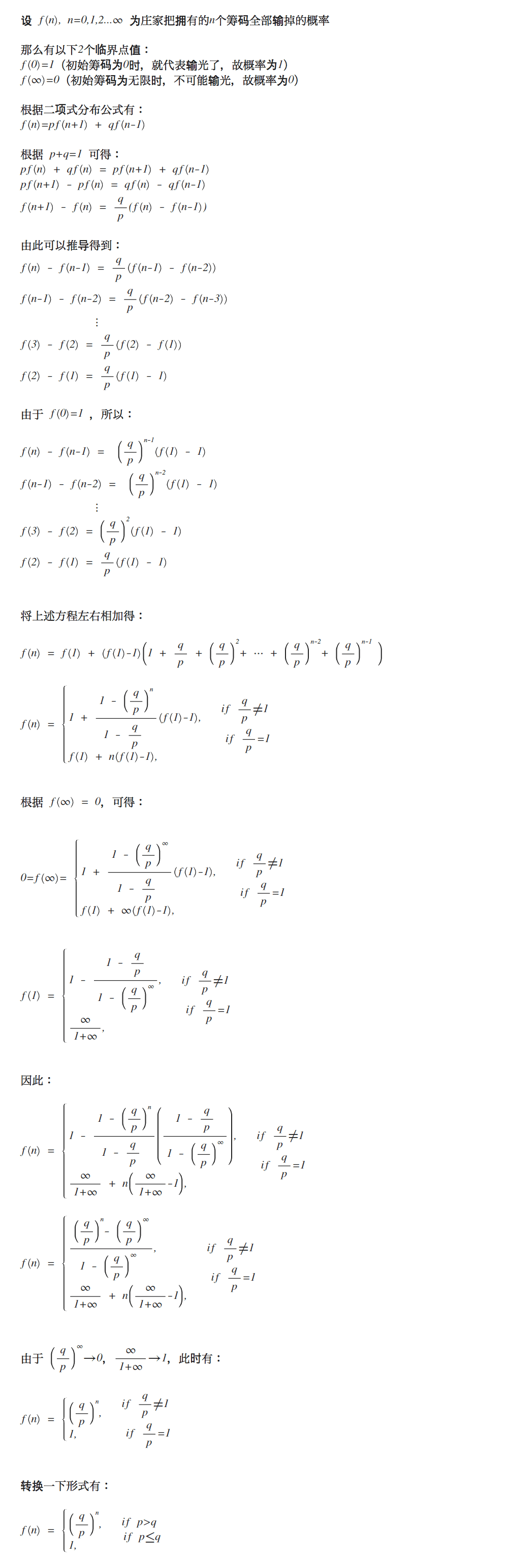
This is the two-dimensional graph of the above mathematical formula:

From the formula and graph, we can conclude:

When p < q, the banker will inevitably lose all chips.
When p >= q, with the same p, the more money the banker has, the smaller the probability of losing all chips.

Probability of the Gambler Winning N Chips#

A gambler starts with n chips, and each time has a probability p of winning a chip or a probability q (q=1-p) of losing a chip. The game ends when the gambler wins N chips or loses all their money. Assuming each gambling instance is independent, find the probability that the gambler wins N chips before losing their initial chips.

The answer is as follows:

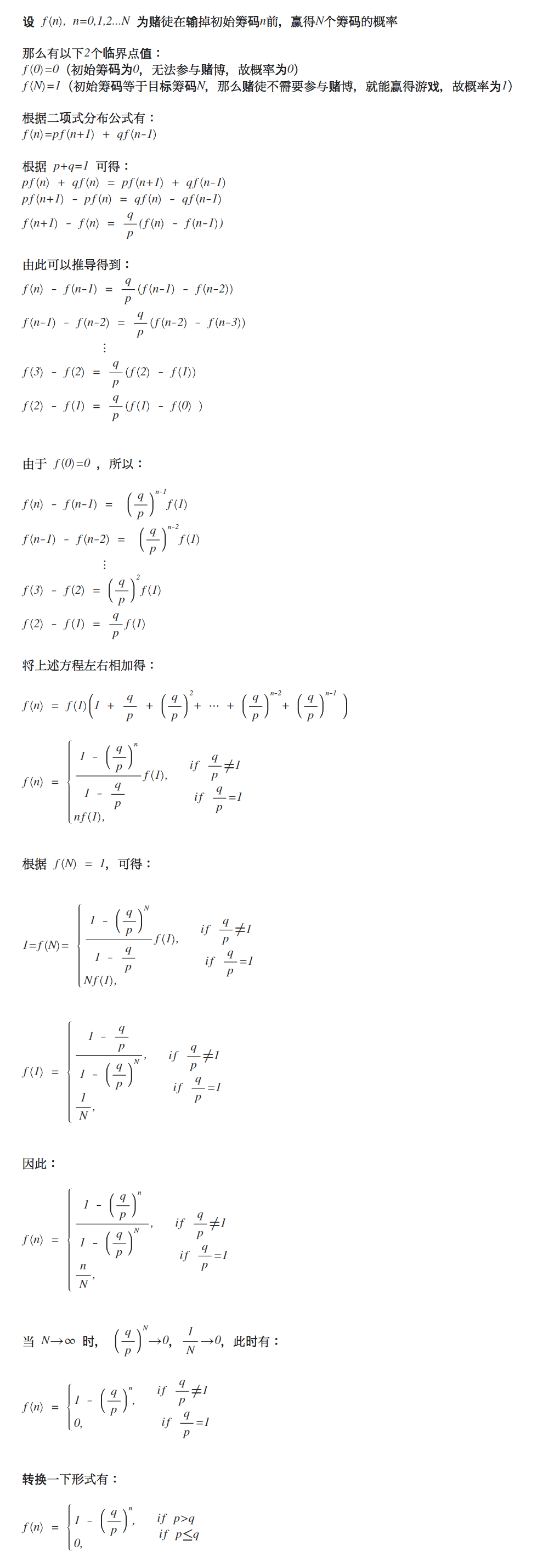
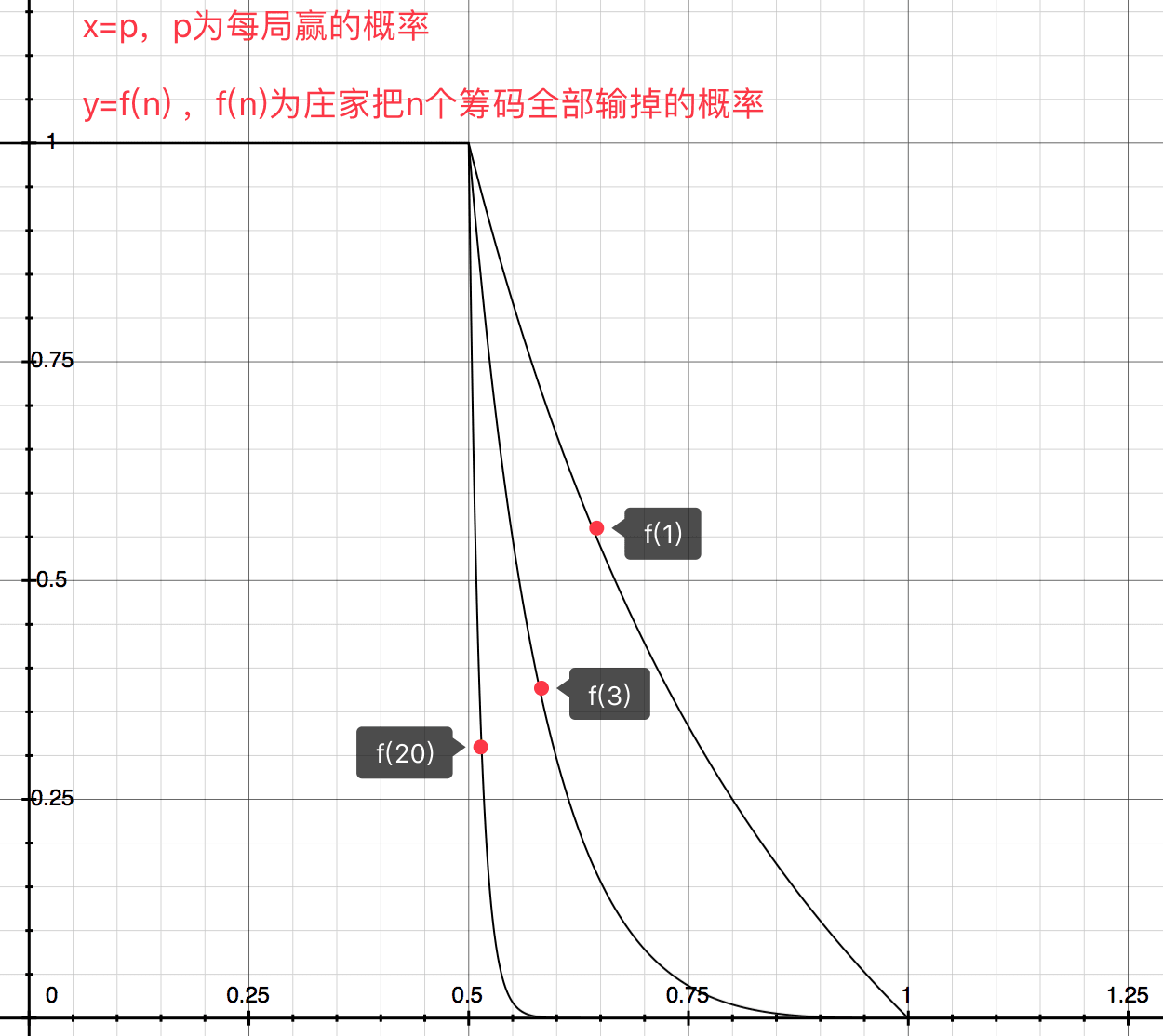
This is the two-dimensional graph of the above mathematical formula:

From the formula and graph, we can conclude:

When p <= q, the gambler cannot win the target number of chips.
When p > q, with the same p, the larger the winning target, the greater the probability the gambler will win.

Combining the above mathematical proofs with real-world situations:

The banker's chips are often more than those of an average gambler.
No casino allows a gambler's winning probability to exceed 50% (i.e., p > q).

Once a gambler enters a casino, in front of a wealthy banker, playing a game with less than a 50% win rate, winning is just a beautiful bubble.

If you don't want to lose money, stay away from gambling—this is the only method that guarantees you won't lose money.

The Gambler's Ruin Problem is a classic probability theory problem, usually used to describe the probability of a gambler going bankrupt when facing a series of gambling outcomes. The basic framework of the problem is:

Problem Description:#

A gambler starts with a certain initial amount and gambles, with the outcome of each gamble being:

If they win, the gambler's wealth increases by a fixed amount (e.g., 1 yuan).
If they lose, the gambler's wealth decreases by a fixed amount (e.g., 1 yuan).

The gambler continues to gamble until they either go bankrupt (wealth drops to 0) or reach a target amount (e.g., reach N yuan). We are concerned with the probability of the gambler going bankrupt, i.e., whether the gambler can reach the target amount before their wealth drops to 0.

Mathematical Model:#

Assuming the gambler's initial wealth is ( x ), the target amount is ( N ), and the outcome of each gamble is either "win" or "lose," with probabilities:

The probability of winning is ( p ) (usually considered to be 0.5 in a fair game).
The probability of losing is ( q = 1 - p ).

Probability of Bankruptcy (in the simple case ( p = q = 0.5 )):#

In symmetric gambling (where ( p = q = 0.5 )), assuming the gambler starts with an initial wealth of ( x ) and aims for ( N ), the probability of bankruptcy (i.e., the probability of reaching the target amount before going bankrupt) can be calculated using the following formula:

Bankruptcy Probability ( P_{\text{ruin}}(x) ):
[
P_{\text{ruin}}(x) = \frac{N - x}{N}
]

This formula indicates the probability of bankruptcy starting from an initial wealth of ( x ).

Asymmetric Gambling (when ( p \neq 0.5 )):#

If the gambling game is not symmetric (i.e., ( p \neq q )), the probability of bankruptcy will differ. In this case, the formula for bankruptcy probability is:
[
P_{\text{ruin}}(x) = \frac{(q/p)^x - (q/p)^N}{1 - (q/p)^N}
]
Where ( q/p ) is known as the "odds ratio." When ( p > q ), the gambler is relatively more likely to reach the target wealth, and the probability of bankruptcy is smaller; conversely, when ( p < q ), the probability of bankruptcy is greater.

Key Conclusions:#

In fair gambling (( p = q = 0.5 )), the probability of bankruptcy depends on the ratio of initial wealth to target wealth. The smaller the initial wealth relative to the target, the greater the probability of bankruptcy.
In unfair gambling, if ( p > q ), the gambler has a better chance of reaching the target wealth. Conversely, if ( p < q ), the gambler faces a greater risk of bankruptcy.

Real-World Applications:#

The Gambler's Ruin Problem is not just a mathematical probability model; it has wide applications in many real situations:

Financial Markets: In investment processes, if the probabilities of asset price increases and decreases are uneven, investors may face similar bankruptcy risks.
Gambling and Games: It is often used to analyze the bankruptcy risks in casinos, lotteries, and other games.
Resource Management: In situations with limited resources, how to balance risk and return to ensure resources can be sustained without depletion.

This problem is a classic application of stochastic processes and Markov chains, revealing how to predict long-term behavior through probability in random events.

This is a classic stochastic process problem, often referred to as the Gambler's Ruin Problem. We need to calculate the probability that a gambler wins ( N ) chips before losing all their initial chips.

Problem Description:#

Initial chips: ( n )
Target chips: ( n + N ) (the gambler needs to win ( N ) chips)
Each gamble: there is a probability ( p ) of winning 1 chip, or a probability ( q = 1 - p ) of losing 1 chip.
Termination condition: the gambler either wins ( N ) chips or loses all their initial chips (i.e., ends up with 0 chips).

Solution Steps:#

Define State:
Assume the gambler has ( x ) chips (where ( 0 \leq x \leq n+N )), define ( P(x) ) as the probability that the gambler starting with ( x ) chips ultimately wins ( N ) chips (i.e., reaches ( n + N ) chips).
Boundary Conditions:
- ( P(0) = 0 ): If the gambler has no chips left, they cannot win ( N ) chips.
- ( P(n+N) = 1 ): If the gambler has already won ( N ) chips, the probability is 1.
Recursion Relation:
At state ( x ), the gambler has two possibilities:
- With probability ( p ), they win 1 chip and move to state ( x+1 ).
- With probability ( q ), they lose 1 chip and move to state ( x-1 ).
Therefore, the recursion relation can be written as:
[
P(x) = p \cdot P(x+1) + q \cdot P(x-1)
]
This indicates that starting from state ( x ), the gambler has a probability ( p ) of moving to state ( x+1 ) and a probability ( q ) of moving to state ( x-1 ).
Solve the Recursion Relation:
This recursion relation is a linear difference equation, and its solution form depends on the size of ( p ) and ( q ). We will discuss two cases:
- When ( p = q = 0.5 ):
  If the probabilities of winning or losing are equal, this problem becomes a simple random walk problem. By solving the recursion relation, we can obtain:
  [
  P(x) = \frac{x}{N}
  ]
  This means the probability that the gambler starting with ( x ) chips wins ( N ) chips is ( \frac{x}{N} ).
- When ( p \neq 0.5 ):
  The solution to the recursion relation is an exponential form. Assuming the solution is ( P(x) = A r^x ), substituting into the recursion relation gives:
  [
  r = \frac{q}{p}
  ]
  Thus, the general solution is:
  [
  P(x) = A \left( \frac{q}{p} \right)^x
  ]
  Using the boundary conditions ( P(0) = 0 ) and ( P(n+N) = 1 ), we can find the constants ( A ) and the specific solution. Ultimately, the probability that the gambler starting with ( x ) chips wins ( N ) chips is:
  [
  P(x) = \frac{1 - \left( \frac{q}{p} \right)^x}{1 - \left( \frac{q}{p} \right)^{n+N}}
  ]
  where ( q = 1 - p ).

Conclusion:#

When ( p = 0.5 ), the probability that the gambler starting with ( x ) chips wins ( N ) chips is:
[
P(x) = \frac{x}{N}
]
When ( p \neq 0.5 ), the probability that the gambler starting with ( x ) chips wins ( N ) chips is:
[
P(x) = \frac{1 - \left( \frac{q}{p} \right)^x}{1 - \left( \frac{q}{p} \right)^{n+N}}
]
where ( q = 1 - p ).

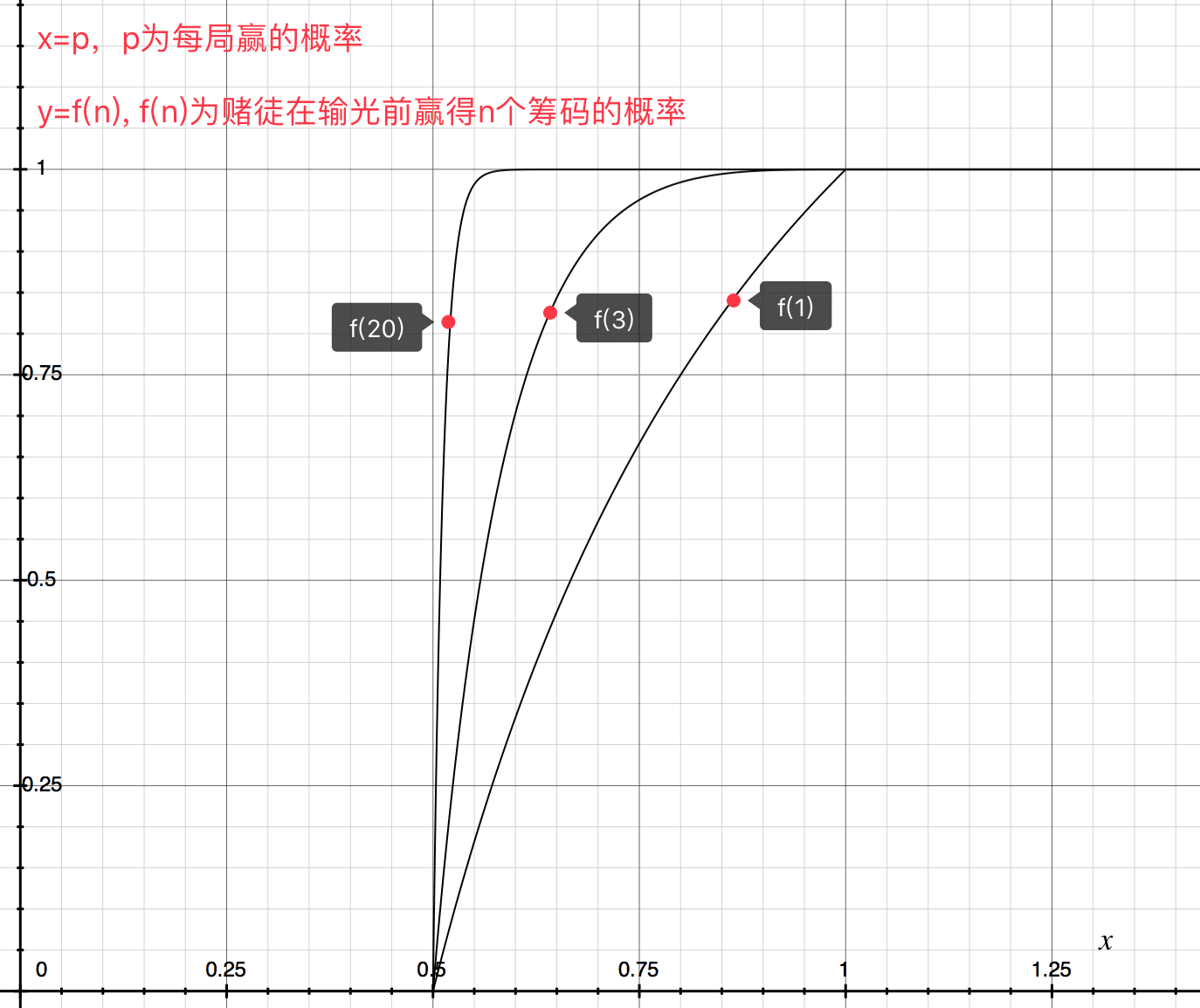
From the formula and graph, we can conclude:

When p <= q, the gambler cannot win the target number of chips.
When p > q, with the same p, the larger the winning target, the greater the probability the gambler will win.

The text you provided describes some conclusions about the Gambler's Ruin Problem. This problem is often used to study the probability of a gambler going bankrupt when starting from an initial number of chips and ultimately aiming to reach a target number of chips.

Explanation:#

When ( p \leq q ), the gambler cannot win the target number of chips:
Here, ( p ) and ( q ) represent the probabilities of winning and losing a single bet, respectively (i.e., ( p + q = 1 )). If ( p \leq q ), the gambler's probability of winning is less than or equal to their probability of losing. In other words, the gambler's expected return is negative, so they are unlikely to reach the target number of chips. Statistically, the gambler is more likely to lose all their chips than to win the target number.
When ( p > q ), the gambler has a greater chance of reaching the target number of chips, and the larger the target number, the greater the probability of winning:
This means the gambler has a higher probability of winning each bet, thus increasing their chances of reaching the target number of chips. Specifically, if the target number of chips is larger, the gambler can achieve this through multiple small wins, which increases their overall probability of success.

Mathematical Background (if more specific formulas are needed):#

The probability of winning the target number of chips:
In the Gambler's Ruin Problem, let the initial number of chips be ( X_0 = x ) and the target number of chips be ( X_T = T ), with the probability of winning each bet being ( p ) and losing being ( q ).

For a general Gambler's Ruin Problem, if the target ( T ) is large and ( p > q ), the probability of the gambler reaching ( T ) can be expressed as follows:

[
P(\text{win}) = \frac{1 - \left(\frac{q}{p}\right)^x}{1 - \left(\frac{q}{p}\right)^T}
]

where ( x ) is the initial number of chips and ( T ) is the target number of chips, and ( p > q ) implies that ( \frac{q}{p} < 1 ), ensuring that both the numerator and denominator of the formula guarantee the gambler's probability of winning the target number of chips increases with the target.

In summary, the gambler's success probability is not only related to the win rate of each bet (the values of ( p ) and ( q )) but also closely tied to the relationship between the target number of chips and the initial number of chips.

How to Research Companies#

Fang Sanwen believes that researching a company can be summarized in three key aspects:

Whether the industry can sustain growth.
Whether the business model has advantages and barriers.
Whether the company's governance structure and the founder's character have advantages.

Industry#

The book discusses many case studies, and the one that impressed me the most is the mobile internet. This is an industry I have personally experienced; I was among the first iOS developers and witnessed the rapid development of mobile internet from its inception in 2010 over the past decade.

In fact, the impact of mobile internet on the entire industry is enormous, but I was not sensitive to it while being in the midst of it. Essentially, it is about having a screen that is always online. This has greatly changed the convenience, real-time nature, and personalized, location-based content display of information exchange.

Company Governance#

Fang Sanwen introduces how he researched BYD's corporate governance:

Observing at BYD's 4S store, interacting with salespeople and customers.
Inquiring about BYD's procurement system from suppliers.
Checking whether the company's external commitments have been fulfilled.

For some companies, the governance structure is relatively less important, which instead highlights the high barriers of such companies, like Moutai.

Valuation#

The book again mentions the "Discounted Cash Flow (DCF) method," which I first saw in an interview article with Duan Yongping.

Discounted cash flow (DCF) aims to determine the intrinsic value of an asset by discounting all future cash flows to present value. There are many related introductory articles, such as this one on Zhihu.

My answer is:
Find good companies (with a long-term perspective); encounter suitable buying opportunities (relying on luck and patience); hold (based on understanding of the company and market fluctuations).
Let me elaborate:

(1) I believe buying stocks is buying companies; the main work investors can do is to find quality companies, which may have good industry positions, good business models, excellent governance structures, and corporate cultures. Given that everyone's capabilities are different, the number of quality companies each investor can recognize is very limited; having ten or eight in a lifetime is already a lot. The discussion about companies in this book is essentially the process of finding excellent companies.
(2) Ideally, being able to buy quality companies at suitable or discounted prices is best, but this is not easy, so it relies on luck and patience, for example, when the entire market is undervalued or when a specific stock experiences a "black swan" event. Investors can hope for good luck to seize such opportunities, but they should not fantasize about always having such opportunities. The book contains a lot of content about market and individual stock buying opportunities, and the conclusion is simple: perfect buying opportunities are rare.
(3) Long-term holding of quality companies is necessary to achieve sufficiently large returns. So how to achieve long-term holding? Two points need to be emphasized: first, understanding the company; only by believing in the company's long-term value can one hold for the long term; second, understanding market fluctuations; realizing that market fluctuations cannot be grasped will prevent one from attempting to "buy low and sell high" to make money from the market. The part of this book about the market mainly explores the relationship between investors and the market, concluding that stock price fluctuations cannot be predicted, and investors should give up the attempt to make money from the market.
(4) If one lacks the ability to find excellent companies and the patience to wait for suitable buying opportunities, does that mean one cannot invest? Not necessarily; the part of this book about asset allocation discusses asset allocation as the most suitable investment method for non-professional investors, and the conclusion is relatively simple: if you don't time the market or select stocks, you will outperform most people.

Chatting and "gambling" are both good life experiences. Of course, there are also unpleasant times, mainly because everyone forgets that what is valuable is discovering one's own foolishness, rather than proving oneself to be great. This can be troublesome.

If so, I have a way to handle it:

Reflect on others
Reflect on companies
Reflect on oneself

Based on my years of "gambling" experience, many who reflect on points 2 and 3 make money, while those who reflect on point 1 rarely do.

Asset Management Framework#

Good Industry (Business Model)
- Mid-level research, the goal is to establish a stock pool.
Good Company (Management Culture)
- Micro-level research, the goal is to establish a stock pool.
Good Price (Timing the Buy)
- Balanced allocation (across categories/markets) to create a base position, avoiding single-point timing risks.
- Increase equity positions when undervalued (very difficult).
- Increase individual stock positions during "black swan" events.
- Buy during market reactions lagging behind fundamental changes (business explosions), increasing individual stock positions.
Holding
- Enjoy corporate appreciation.
- Reinvest dividends.
Selling
- Sell when confirming errors in industry or company judgments.
- Sell individual stocks that exceed position limits (not necessarily correct).
- Reduce equity positions when the stock market is generally overvalued (very difficult).

The real change is in people's perspectives and experiences; looking back, there are many opportunities; looking forward, there are few opportunities. Beautifying the past is a human thinking habit, and the logic behind it is that people find it much easier to summarize and understand things that have already happened than to analyze the ever-changing current situation and predict possible future directions.

The Impossibility in the Stock Market#

Everyone makes money.
Everyone is a value investor.
Stock prices are all "reasonable."
Major shareholders never reduce their holdings.
There is a stock god who sees through all price fluctuations.
There is a technique or tool that can accurately predict the stock market.
Financial statements fully reflect the company's operating status.
Listed companies only distribute dividends and do not raise funds.
The entire stock market is composed entirely of quality enterprises.
All investors know the company's information simultaneously.
There is no insider trading.
Lessons are learned, and mistakes are not repeated.
Everyone buys the dip, and everyone sells the peak.
There is an omnipotent "banker" manipulating a stock.

Market Quotes#

(1) Most "value investors" are actually speculators in popular stocks.
(2) Ways to control drawdowns:

Major asset allocation and rebalancing; 2) Try to hold companies with weak performance cycles; 3) Buy cyclical stocks counter-cyclically; 4) Use pseudo "black swan" events to buy.
(3) Gains and losses come from the same source; a fund that performs particularly well in a certain year may have a large portion of its profits as a bubble, which is easy to return, so finding the reason is very important.
(4) Value investing has little to do with the price-to-earnings ratio. Many who buy stocks at a price-to-earnings ratio of 100 are truly value investors; many who buy stocks at a price-to-earnings ratio of 10 are not value investors.
(5) Investment is about investing expectations.
(6) Stock market crashes are necessary once or twice a year.
(7) What is the greatest freedom in the capital market? It is that you can buy or not buy; whether it is subscribing at IPO or voting during privatization, no one can force you to make a choice, so you must cherish this right and fully bear the consequences of your choices.
(8) If you find the management unreliable after buying a company's stock, the only answer is: "You bought it wrong." Questioning the character of the management is meaningless.
(9) You need to have a sufficient understanding of your investment targets and establish valuations in your mind, so that market fluctuations have nothing to do with you. If you let market fluctuations lead you, then investing or trading stocks will be a hard job for you, and you will definitely not make money in the end. So why bother to make things difficult for yourself?
(10) Those who base their investment on valuation can successfully "sell at the top" and "buy at the bottom," because the top must be when stocks are too expensive, and the bottom must be when stocks are too cheap. Those who think about selling at the top and buying at the bottom all the time often end up selling on the slope and buying in the middle.
(11) For mainland investors, the easiest rich mine to dig is still the mainland consumer companies listed in Hong Kong, which have excellent qualifications and valuations much lower than A-shares.
(12) "Bubbles are not punctured; they are burst by being too large." Human nature has never changed, so there is nothing new under the sun.
(13) Whether it's an IPO or a private placement, if you think it's overpriced and don't want to buy, if it can be issued, it means others want to buy; that is their freedom. Restricting IPOs and private placements essentially aims to limit others' investment freedom, forcing them to use their money to buy your overpriced goods. This kind of thinking is unfair.
(14) The market is fair; the rules apply equally to anyone (regardless of wealth), which is the hallmark of a healthy market.
(15) Other things are hard to say, but the payment rate on mobile is definitely much higher than on PC; this is a profound lesson the mobile internet has taught me.
(16) Health products are basically useless, but the demand for health products is real, so health products are a good business.
(17) You think you are fighting against "short sellers," "trolls," and "stock bears," but in reality, you are fighting against your own foolishness, greed, and fear.
(18) In my view, trying to concentrate and always being fully invested is a more conservative strategy, but others will probably think I am a radical "madman."
(19) Wanting to sell when something is expensive essentially means wanting to make money from the market, which belongs to a kind of overreaching greed.
(20) High-margin products can only be products that satisfy spiritual needs or products whose functions cannot be verified, falsified, or quantified.

Asset Management Framework#

Good Industry (Business Model)
- Mid-level research, the goal is